Cross-Validation

Why

When you have training set and test set for model selection, one idea would be use the training set to estimate parameters for each model candidate, and then choose the model generates the least error to test data.

However, an extra parameter was chosen using the test set -> the generalisation error is underestimated.

How

• split the data set into:
  • training set
  • cross validation set (= validation/development/cv set)
  • test set
• the ratios
  • traditionally, the ratios are train-dev-test = 70%-20%-20%
  • for large data set or in deep learning, the ratios can be train-dev-test = 98%-1%-1%
  • the dev and test sets should have similar distributions
• correspondingly, you will have training error, cross validation error, and test error (i.e. Cost Functions without regularization terms)

Types of cross-validation techniques

• Leave p out cross-validation ( (LpOCV)
  • using $p$ observation as validation data
• Leave one out cross-validation
  • a special case of LpOCV where $p=1$
• Holdout cross-validation
  • such as 70% for training, 30 % for testing
• k-fold cross-validation
  • It divides the sample in a number of chunks, called “folds.” The model is asked to predict each fold, after training on all the others.
  • How does it work:
    • equally partition data into k subparts or folds
    • -> out of the k-folds or groups, for each iteration, one group is selected as validation data, and the remaining (k-1) groups are selected as training data
    • -> iterate k times
  • The final accuracy of the model is computed by taking the mean accuracy of the k-models validation data.
• Stratified k-fold cross-validation
  • = a k-fold cross-validation for imbalanced dataset
• Repeated random subsampling validation (Monte Carlo cross-validation)
  • It splits the dataset randomly into training and validation
  • The number of iterations is not fixed and decided by analysis.
  • The final accuracy of the model is computed by taking the mean accuracy over the splits.
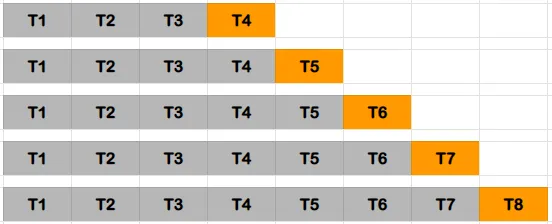
• Time Series cross-validation
  • It splits data into train and validation according to the time: forward chaining method or rolling cross-validation
  • The chance of choice of train and validation data is forwarded for further iterations:
• Nested cross-validation
• An improved cross-validation: Pareto-smoothed importance sampling cross-validation (PSIS)

Example: cross-validation for model selection

1. determine model options: number in polynomial/number of layers in neural network...
2. compute the model that generated least cross validation errors
3. then estimate the generalization error of the test set