What does Gradient Descent do

It minimizes cost function using derivatives by proceeding in epochs (an epoch consists of using the training set entirely to update each parameter).

Adaptive methods

The adaptive methods in gradient descent can automatically adjust the learning rate.

• Newton's method
  • computes and uses the full Hessian
  • works for convex problems but needs adjustments for nonconvex problems
• preconditioning
  • avoids computing the Hessian in its entirety but only computes the diagonal entries

Gradient descent in Neural networks

• use forward-propagation to calculate the values of each layer
• use back-propagation to calculate the derivatives
• example of a two-layer logistic regression neural network by Andrew Ng:
  

Variants of Gradient Descent

Variants Outline:

• #Batch gradient descent

• #Stochastic gradient descent (SGD

• #Mini-batch gradient Descent

• #Momentum

• #RMSprop (Root Mean Square prop)

• #Adam (Adaptive Moment Estimation)

• #Learning rate decay

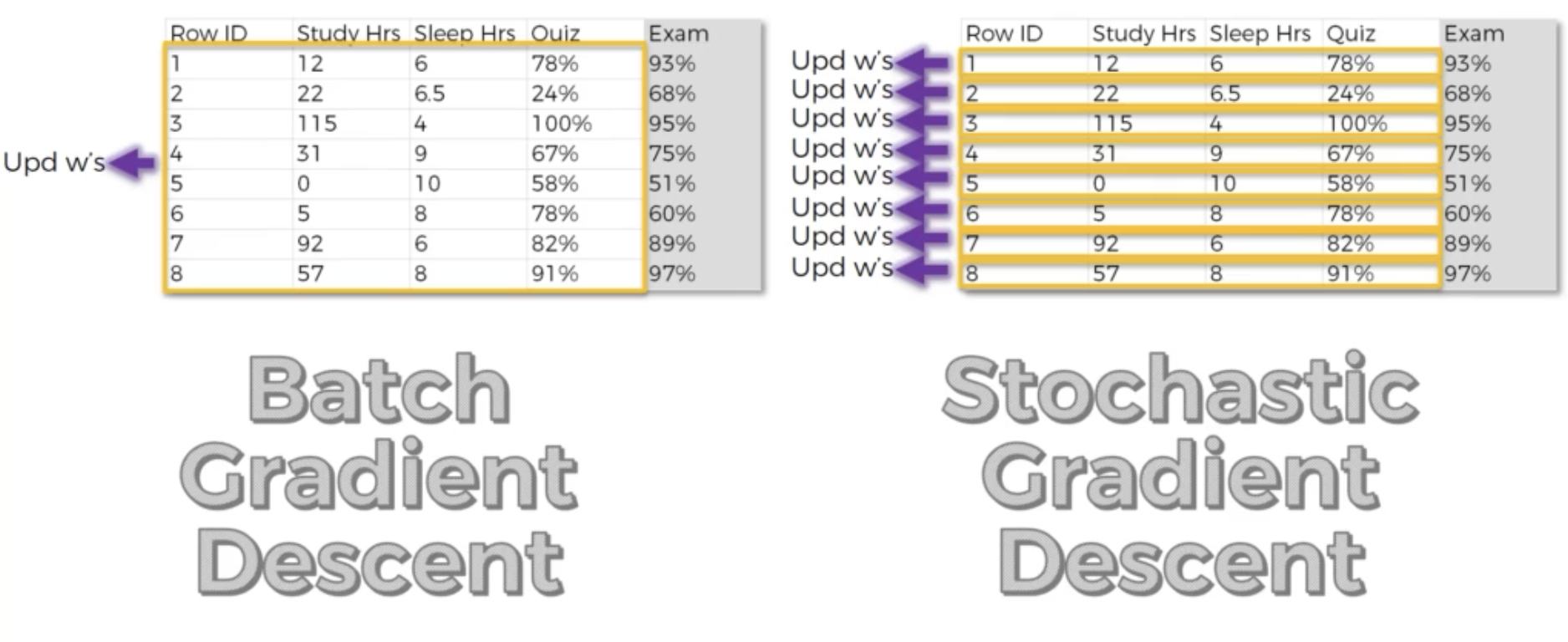
Batch gradient descent

• most basic approach
• the loss function= an average of the losses computed on every single example in the dataset

Stochastic gradient descent (SGD）

• a variant of batch gradient descent where the weights are updated after computing the gradient of the loss function with respect to a single training example at a time
• while each individual observation will provide a poor estimate of the true gradient, given enough randomness the parameters will converge to a good global estimate
• SGD itself has various “upgrades” variants
  • AdaGrad
    • a version of SGD that scales $\alpha$ for each parameter according to the history of gradients. As a result, $\alpha$ is reduced for very large gradients and vice-versa
    • used per-coordinate scaling to allow for a computationally efficient preconditioner
  • Momentum (Gradient Descent#Momentum): helps accelerate SGD by orienting the gradient descent in the relevant direction and reducing oscillations
  • RMSprop (Gradient Descent#RMSprop (Root Mean Square prop)) and Adam (Gradient Descent#Adam (Adaptive Moment Estimation)): frequently used in neural networks

Batch gradient descent vs. Stochastic gradient descent

• batch ones are slow; stochastic ones can avoid local minimum but can be noisy and computationally inefficient
• different ways to update weights
  

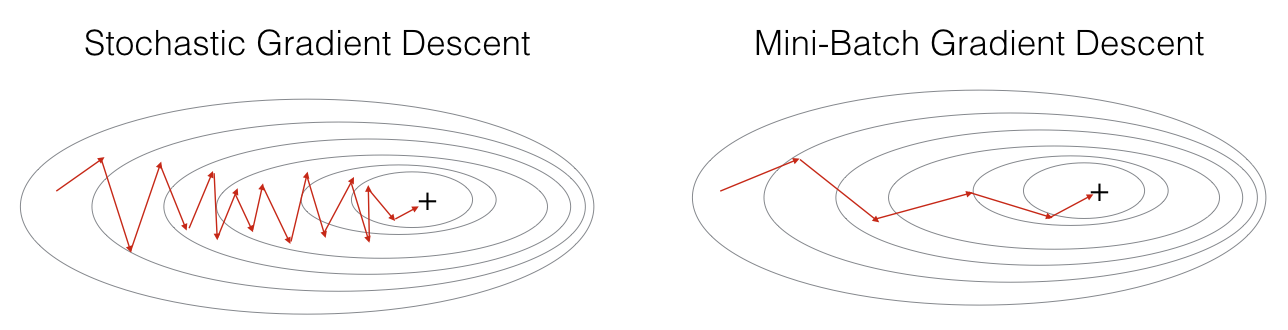
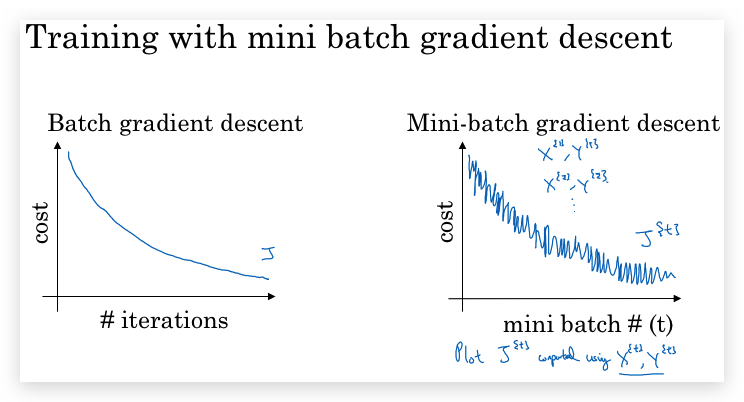
Mini-batch gradient descent

• Mini-batch a compromise between batch and stochastic gradient descent, where the weights are updated after computing the gradient of the loss function with respect to a small batch of training examples (typically between 32 and 512).
• efficient multi-machine, multi-GPU and overall parallel processing
• Comparison: SGD vs. mini-batch gradient descent
  
  
• when to use
  • when the data size is very large (>= 2000)
• what to use
  • if $n_{batch}$ = m: batch gradient descent
  • if $n_{batch}$ = 1: stochastic gradient descent
  • usually $n_{batch}=2^n$: 64, 128, ...
• it should fit in CPU/GPU memory

Exponentially weighted averages

(Exponentially weighted moving averages)

• describes the trend using local averages

Momentum

• The idea behind gradient descent with momentum is to add a "momentum" term to the weight update rule (stochastic gradient descent) that encourages the weight updates to continue in the same direction as the previous updates
• it aggregates a history of past gradients to accelerate convergence and reduce oscillations in the optimization process
• The weight update rule for gradient descent with momentum can be written as:

where v(t) is the "velocity" vector at time t, $\gamma$ is the momentum coefficient (typically set to a value between 0.9 and 0.99), learning rate is the step size or learning rate, gradient is the gradient of the loss function with respect to the weights, and weight(t) is the weight vector at time t.

RMSprop (Root Mean Square Prop)

• it works by maintaining a moving average of the squared gradients and using that to scale the learning rate
• it decouples per-coordinate scaling from a learning rate adjustment
• coefficient $\gamma$ determines how long the history is when adjusting the per-coordinate scale

Adam (Adaptive Moment Estimation)

• Adam is a combination of two other optimization algorithms, namely, stochastic gradient descent with momentum and RMSprop.

Learning rate decay

• reduce the learning rate over time as the optimization process progresses.
• the idea behind learning rate decay is that as the algorithm gets closer to the minimum of the loss function, it may benefit from smaller steps to avoid overshooting or oscillations around the minimum.
• can be combined with other algorithms such as SGD and Adam