Regularization
Regularization
What is regularization
- Regularization = the process of adding information in order to solve an ill-posed problem or to prevent overfitting.
- Intuition:
Increasing the regularization parameter( >0) reduces overfitting by reducing the size of the parameters. For some parameters that are near zero, this reduces the effect of the associated features.
Alternative intuition for deep neural networks:
Regularization reduces overfitting by letting the weight of units decay and get closer to 0 (given thatare usually large). If the weights almost zero, than the networks becomes almost linear and will avoid overfitting.
Cost function with regularization
When you choose regularization, a regularization term will be added to the cost function.
See Cost Functions#Cost function with regularization.
Types of Techniques
- shrinking (= add penalty/reduce weight/weight decay)
-
L1 regularization (lasso): Cost Functions#^19a2bf
-
L2 regularization (ridge, "weight decay"): Cost Functions#^b2a01f
-
elastic net regularization
- = L1 + L2 regularization:
-
, where
-
dropout regularization
- randomly knocking out units in neural network
- used only during training
- mostly used in computer vision (e.g. Pattern Recognition)
-
batch-normalization
-
data augmentation
- usually in computer vision
- = generate more labeled images by taking labeled images and
- flip them left/right
- shift them up/down/right/left by a couple pixels
- add small noise, etc...
- but if the validation set doesn't have the same randomness, then the accuracy fluctuates crazily.
-
early stopping
- Initialize with small weights -> these get bigger as you do gradient descent- > stop when they are the ‘optimal’ size
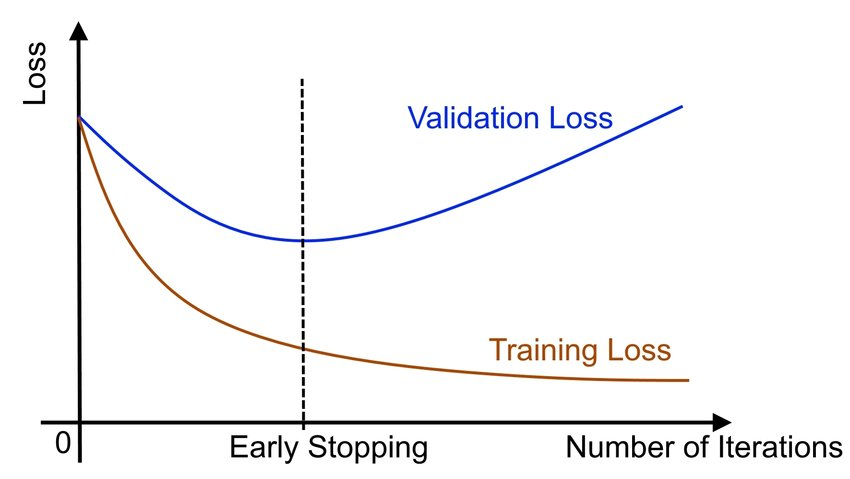
But long-term training may lead to flip in large models, see here
Regularization in Bayesian framework
- A regularizing prior is a "skeptical" prior, which means it slows down the rate of the model in learning from the data.
- Multilevel models can be regarded as adaptive regularization, where the model itself tries to learn how skeptical it should be.
- It is a Bayesian method. It is the same device that non-Bayesian methods refer to as “penalized likelihood.”